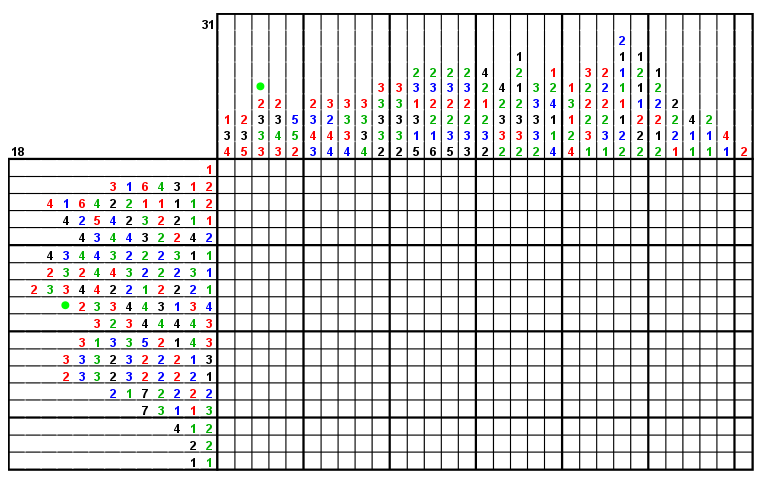
Nonogram solving has become a standard test problem for designers of constraint solving systems. Typically only black-and-white nonograms are considered. I thought it might be interesting to see how the approach extends to a slightly more complex problem: multicolor nonograms.
An example of a multicolor nonogram is shown below:

If you'd like to try solving the puzzle above, you can do so on webpbn.com.
| Black & White | Multicolor | ||||||||||||||||||||||
|
|
| Black & White | Multicolor |
Color of cell (i,j):
x(i,j) ∈ { 0,1 }Left-most position of the k-th block in the i-th row: r(i,k) ∈ { 0..n - rows(i)(k) }Top-most position of the k-th block in the j-th column: c(i,j) ∈ { 0..n - cols(j)(k) } |
Color of cell (i,j):
x(i,j) ∈ { 0..nc }Left-most position of the k-th block in the i-th row: r(i,k) ∈ { 0..n - rown(i)(k) }Top-most position of the k-th block in the j-th column: c(i,j) ∈ { 0..n - coln(j)(k) } |
The non-overlapping constraints are the same for pairs of blocks of the same color, but if they are different colors the '<' sign becomes a '≤' because there does not need to be a separating white space.
The covering constraints for black and white puzzles said that a cell could be black if and only if it was covered by a block. We say instead that a cell can be a given color if and only if it is covered by a block of that same color.
| Black & White | Multicolor |
Row blocks do not overlap:
r(i,k)+rows(i)(k) < r(i,k+1)Column blocks do not overlap: c(j,k)+cols(j)(k) < c(j,k+1) |
Row blocks do not overlap:
When rowc(i)(k) = rowc(i)(k+1):Column blocks do not overlap:r(i,k)+rown(i)(k) < r(i,k+1)When rowc(i)(k) ≠ rowc(i)(k+1):r(i,k)+rown(i)(k) ≤ r(i,k+1) When colc(i)(k) = colc(i)(k+1):c(j,k)+coln(j)(k) < c(j,k+1)When colc(i)(k) ≠ colc(i)(k+1):c(j,k)+coln(j)(k) ≤ c(j,k+1) |
The cell (i,j) is black iff it is contained in a row block:
x(i,j)=1 ↔ ∨k (r(i,k) ≤ j ∧ j < r(i,k)+rows(i,k))The cell (i,j) is black iff it is contained in a column block: x(i,j)=1 ↔ ∨k (c(j,k) ≤ i ∧ i < c(j,k)+cols(j,k)) |
The cell (i,j) is color v iff it is contained in a row block of that color:
x(i,j)=v ↔ ∨k : rowc(i,k)=v (r(i,k) ≤ j ∧ j < r(i,k)+rown(i,k))The cell (i,j) is black iff it is contained in a column block: x(i,j)=v ↔ ∨k : colc(j,k)=v (c(j,k) ≤ i ∧ i < c(j,k)+coln(j,k)) |
This set of constraints may appear to be much more complex than the original one, but they really aren't. We have the same number of non-overlapping constraints, but now some contain '≤' signs instead of '<' signs. Originally we had two covering constraints for each grid cell, one for rows and one for columns. Now there are two constraints for each non-background color, but the constraints for color v contain only the disjunctive terms corresponding to the clues of that color, so the total "length" of the constraints is about the same.
It's also important to note that in the special case where the number of non-background colors is one, the multicolor case is identical to the black and white case. That means the multicolor solver shouldn't be significantly slower on black and white puzzles than the original version was.
Debugging proved mildly difficult, since Scala is compiled into Java byte code in such a way that at run time it is unable to report what line of Scala code caused an error. This is obnoxious and stupid, but inserting a lot of print statements into the program made it easy enough to localize the errors. Overall, writing and debugging the program took a couple hours - less time than writing this report.
The complete Scala program is available here.
To compile and run it, you'll need to download the source code zip file from Tamura's page and simply substitute my Scala script for his.
Of course, the input files for the new program are in a different format than the ones for the black and white program, since they need to include clue color data. They are CWC files instead of CWD files, and can be exported from my Webpbn Puzzle Export Page.
When I modified the subroutine that prints out the solution of the puzzle, I did it in a slightly dimwitted way that will not work well for puzzles with more than nine non-background colors, but since webpbn supports only four non-background colors, that will suffice for now. Doing it better would have required learning more Scala.


The color nonogram solver that resulted from this exercise is a lot slower on most puzzles than the pbnsolve program that I wrote from scratch in C, but initial tests indicate that, like Tamura's original black and white puzzle solver, it can solve many more of the rare hard puzzles. In fact, it was able to solve every one of the 13,456 multicolor puzzles I tested it on, though one took over two hours to solve.
The pbnsolve program solves almost as many puzzles, and does the vast majority much faster, but it is the product of years of work and refinement. The Copris solver took me only a few hours to build. Pbnsolve consists of some 9,000 lines of application-specific code, compared to some 120 lines for this program.
I am only aware of about four programs that solve color nonograms, and only two of them are any good at solving hard puzzles. On the other hand, there are dozens of black and white nonogram solvers. If you wanted to extend one of those to work for color puzzles, you'd find yourself rewriting most of it. Data structures would have to change. The line solver algorithm used for multicolor puzzles is a great deal more complex than for black and white puzzles. Search heuristics would have to change.
With Copris, on the other hand, I was able to make the upgrade quite easily, in spite of the fact that I know very little about Scala, less about Copris, and have never previously done any programming with any Constraint Programming System.
Frankly, I think this is gigantic. The ability afforded by modern CSPs to easily build powerful solvers for complex problems is truly amazing, and I strongly suspect that this is a very important part of the future of computer science.