Most people don't seem to need a lot of instruction on how to solve paint-by-number puzzles (or nonograms, griddlers, hanjie, picross, or whatever else you like to call them). The basic solving technique is easily demonstrated in a simple example, such as the one on the front page of this site. I expect most reasonably clever people could figure it out even without being shown. And that basic solving technique is really pretty powerful, and can be used to solve most puzzles. However there are some cases where slightly more elaborate logic tricks are required to solve a puzzle.
This page is meant to give some ideas about fancy paint-by-number solving techniques, and also to establish some terminology for talking about solving techniques in the forums on this site.
"Line solving" is when you work with one row or one column at a time. Sometimes this is simple and straight forward, like the case below, where we know the cells marked "A" must be black:
Sometimes it takes a little thinking about different cases, like in the case below where the single "B" cell must be black:
And sometimes there are things that are pretty darned hard to spot, like the fact that cell "C" in the line below needs to be white:
But though line solving isn't always "simple" in the sense of being easy, it at least always involves looking at only one row or column at a time.
By the way, computer programs written to solve paint-by-number puzzles love line solving. It's just the kind of thing a computer loves - looking at one small part of the problem at a time and hoping that an overall solution will come together out of that. Puzzles that are solvable by line solving alone are almost always easily solvable by computers. It's in the cases where you have to look at more of the puzzle to figure things out that humans can really outsolve the computer programs.
Line solving gets you nowhere on this puzzle.
But the puzzle is symmetrical, in the sense that it is exactly the same as it's mirror image. Each horizontal clue is reversable. "1 1" backwards is "1 1". The top clue in column 1 is the same as the one in column 4, and the top clue in column 2 is the same as column 3.
Clearly if you found a solution to this puzzle, and reflected the solution around a vertical axis, then that mirror image would also be a solution to the puzzle. If there is only one solution, then we know that the solution has to be symmetrical. Knowing that the solution is symmetrical is a really big clue.
Unfortunately, on this web site at least, you can never be sure that a puzzle really only has one solution, and without knowing that, solving using symmetry is a bit of a cheat. We don't normally consider a puzzle "logically solvable" if it can only be solved by symmetry. The exception is that if the author of the puzzle puts some information in the title of a puzzle like "[has only one solution]" then it is completely legitimate to use symmetry to solve the puzzle because that information was given to use as part of the puzzle. (See, for example, puzzle #65.)
Once you know the solution to the puzzle above is symmetrical, it is trivial to solve it. For starters, if any side clue has an odd number of clue numbers in it (like the "2" rows) then the center columns must be black. And if it has an even number of clue numbers, then the center columns must be white. (In this case we have two center columns, but if the puzzle had an odd number of columns, we'd only have one.) That alone is almost enough to solve most symmetrical puzzles.
Of course, there are other forms of symmetry. The puzzle could have vertical symmetry or diagonal symmetry or rotational symmetry (though it would have to be square for either or the last two to hold).
Though solving by symmetry is kind of cheating, it's certainly not a case of looking at just one line at a time. You really have to look at the whole puzzle to detect symmetry.
The most obvious kind of logic that involves looking at row and column clues at the same time is "color logic." This happens in multicolor puzzles when the row clue tells you that a cell must be either color A or color B, while a column clue says that it must be either color B or color C, so we can conclude that it must be color B.
Here's a simple example:
Again, line logic doesn't work, but it's quite obvious that cell "A" has to be white. After all, the row clue says it can only be red or white, and the column clue says it can only be green or white, so it must be white.
Here's a much trickier example:
Again, line solving gets us nowhere, and we'll ignore the rotational symmetry of the puzzle (which is tricky to spot and cheaty to use).
A productive line of reasoning, however is to ask which cells in the second row can be red. By looking at the top clues, we can see that the cells marked with "A" cannot be red. They could be either green or white, but not red. But if that's the case, then cell "B" must be red, and can be marked red, because every place the red three could be includes that cell. The same logic can be applied on the other three sides of the puzzle, and once you've done that, the rest of the puzzle is easy to solve with line solving.
The trick with color logic is remembering which colors each cell can be. Some computer programs, like the "checker" used on this site, keep a list of possible colors for each cell. If you do that, then all the above puzzles become easy to solve by plain old line solving (though the line solving algorithm becomes a bit more complex). Possibly you could invent some system of notation that would let you do the same thing on paper, but I doubt it would really be useful. In practice, it's really just a matter of figuring it out in your head. Tricky, but I don't think example 6 is really trickier than, say, example 3.
"Edge logic" (or "boundary logic") is a logic trick frequently useful along the edges of a puzzle. Puzzle #23 on this site was designed as an example of this sort of thing. It looks like this:
It's hard to imagine a puzzle less ameniable to line solving. Experienced solvers will notice one promising feature immediately however: along the bottom edge there is a fairly big number (the "4") with only small numbers (a "2") in the next row up.
The trick in such cases is to consider those two rows together. Since the "4" row is right on the edge of the puzzle, it's easy to see what the consequences are if the "4" is in different locations and to check if those consequences are consistent with the "2" row. So we just mentally try the "4" in different positions. We might start by supposing that cell "A" was black. Obviously that would mean all the cells marked "B" would have to be black too. Looking at the column clues, we see that the two cells marked "C" would have to be black too. While the cells marked "D" would have to be white. But this makes for an impossible pattern of blacks and whites in that row. There can only be a two in that row. So this means "A" cannot be black and must be white.
Once you get the idea of this, it is quite easy to see that most of the places where you could place the four in the bottom row would produce an impossible pattern in the second row from the bottom. In this puzzle there is actually only one place it can be, which is the position shown below. In any other position it would either give three blacks in the second row, or two blacks with a white in between.
If we want to continue solving this puzzle, then we can apply the same trick again. This time we'd be working with the 4 in column 6. Though in this case we aren't working with the outer edge of the puzzle, we are still doing the same basic thing on the edge of the unknown area.
Edge logic is useful in a lot of puzzles, but it doesn't usually work quite as well as it did in example 7. Often you'll find that there are several different places where the edge block could be. But that still may be enough to allow you to dot a few cells (especially in the corners) and it may be that all possible positions overlap on a few cells that you can paint black.
There are many variations on edge logic. Sometimes the first row inward may prove useless, but the second row inward will be more helpful. Sometimes you can even apply it to the placement of a block in the first row inward by checking consistency with the second row inward.
A good first puzzle to try edge logic on is #6336.
Another pattern that one frequently encounters is the "smile". We call it that because the most common form that it appears in is the smile shaped puzzle below:
The solution, shown at right is unique, but none of the techniques we described above let us solve it (well, symmetry does, but we don't want to use symmetry).
The key to it is all the ones in the column clues. We know that there can be only one black in each column, so we know that the horizontal 1 and 2 blocks never can overlap each other. Since the 1's can't be next to each other either (because we need a white space between them) the blocks from the two rows must alternate. They have to go 1,2,1.
The exact same reasoning applies to the puzzle below, with a solution that looks more like a snake than a smile:
Normally puzzles don't start out with so many columns containing just a one. This is more a kind of situation that sometimes develops in a puzzle that is almost complete, where there were a lot of other clue numbers in the columns, but those have already been placed. Smile logic is something usually used late in the solving process, unlike edge logic which can be applied at any point. (But, for an exception to that rule, see puzzle #6542).
Another common variation of smile logic occurs in situations like the puzzle below:
This puzzle has already been partially solved using classic line solving, but line solving doesn't get us any further. But the eight unsolved squares are really in exactly the same situation as the basic smile pattern in example 8. The same reasoning can be applied to solve this.
The example below is similar to ones I sometime use when I'm otherwise stuck. I haven't got a really clever name for it, but for now I'm calling it "two-way logic". It has been solved as far as line solving will take you. What's not so obvious is that all the cells marked "A" must be white.
The reasoning goes like this. Clearly the "2" block in column 7 can only be in one of two positions. That tells us something about column 6: either the cell directly above the dotted cell, or the one directly below the dotted cell must be black. So the "2" in that column can only be in one of two positions, which don't include any of the "A" cells, so we can dot them all. From there the rest of the puzzle solves easily. (Actually example 11 isn't all that cleverly designed because it can also be solved by edge logic.)
So the basic idea here is to look for places where you know one of two cells must be black. For each case think just a move or two ahead, to see what other cells you could set in that case. If any cells get set the same way in both cases, then you can mark them.
A slightly different example of the same trick is shown below. Using two-way logic on the two open cells in column seven lets you set exactly one cell, which makes the rest of the puzzle solve:
Did you find it? It's the cell in the fourth row, and sixth column and it has to be white. If the "2" in column seven is in the upper position, then all the rest of of row four must be white. If the "2" is in the lower position, then the top half of column six must be white. Either way, that one cell must be white.
Again, it happens that this puzzle can also be solved by edge logic. It's hard to contive small puzzles that can only be solved by two-way logic.
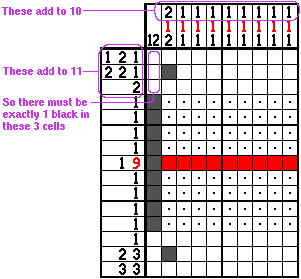
Sometimes interesting things can be achieved by adding up how many cells need to be set in a particular region. Here's a puzzle contrived to demonstrate this trick:

We've used simple line solving to fill in a lot of space, but we've got unsolved regions at the top and the bottom still to figure out. The next thing we'd naturally try to complete this puzzle would be edge logic on the 12 in column one, but that doesn't get us anything.
But there is a simple trick that will tell us exactly where the 12 needs to be. First, use the row clues to add up the number of cells that are needed in the top three rows. The first row is 1+2+1=4, the second is 2+2+1=5, and the third is just 2, so the total is 4+5+2=11. We need a total of 11 black cells in the top three rows of the puzzle.
Now, if we look at the column clues, we can use them to figure out how many cells there are in the top three rows for every column except column one. Column 2 must have 2 cells, and the other eight columns must have one each, for a total of 10.
So, since the row clues tell us there must be 11 cells filled in, in the top, and since we know there are 10 in columns 2 through 10, there must be exactly one black cell in the first three rows of column 1. That tells us exactly where the 12 in column 1 must be, and the rest of the puzzle is trivial to solve.
I've only ever used this trick on a handful of actual puzzles, but it's nifty when it works out.
Obviously this isn't an exhaustive list of every fancy logic trick that is useful in solving paint-by-number puzzles. Sometimes you have to invent a new one from whole cloth to solve a puzzle. But hey, that's fun, isn't it?
Of course, some people prefer to just guess if the going gets tough. If that makes you happy, then it's OK with me, I guess.